进制转换

可以参考数电内容，这里不再赘述。

技巧：二进制转十六进制

• 例：101111.001 因为 $16 = 2^4$，所以每4位二进制数对应1位十六进制数。$0010,1111.0010$ 分别转换得到 2,F,2即 $2F.2_{16}$

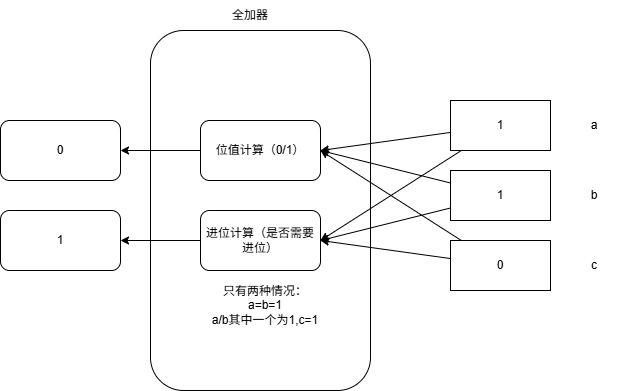
二进制计算比较简单，只有四种情况

表：2进制1位加法

a	b	res
0	0	0
0	1	1
1	0	1
1	1	0 (进位)

两数相同为0，不同为1

与或非

A	B	Y
0	0	0
0	1	0
1	0	0
1	1	1

与门（AND）

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	1

或门（OR）

更多逻辑门

与门+非门=与非门（NAND）

A	B	Y
0	0	1
0	1	1
1	0	1
1	1	0

与非门（NAND）

或门+与非门+非门=异或门（XOR）

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

异或门（XOR）

异或门：两输入不同时输出1，相同时输出0 我们发现这与二进制的加法是完全一致的。 我们还可以添加一个与门来实现二进制的进位。

全加器和并行加法器

比如1101+0110. 还是一样，从低位到高位开始计算。

  1 1 0 1
+ 0 1 1 0
-----------
  0 0 1 1

从后往前，每一次计算的结果作为下一次计算的进位输入，然后连同前面两位一起使用全加器计算。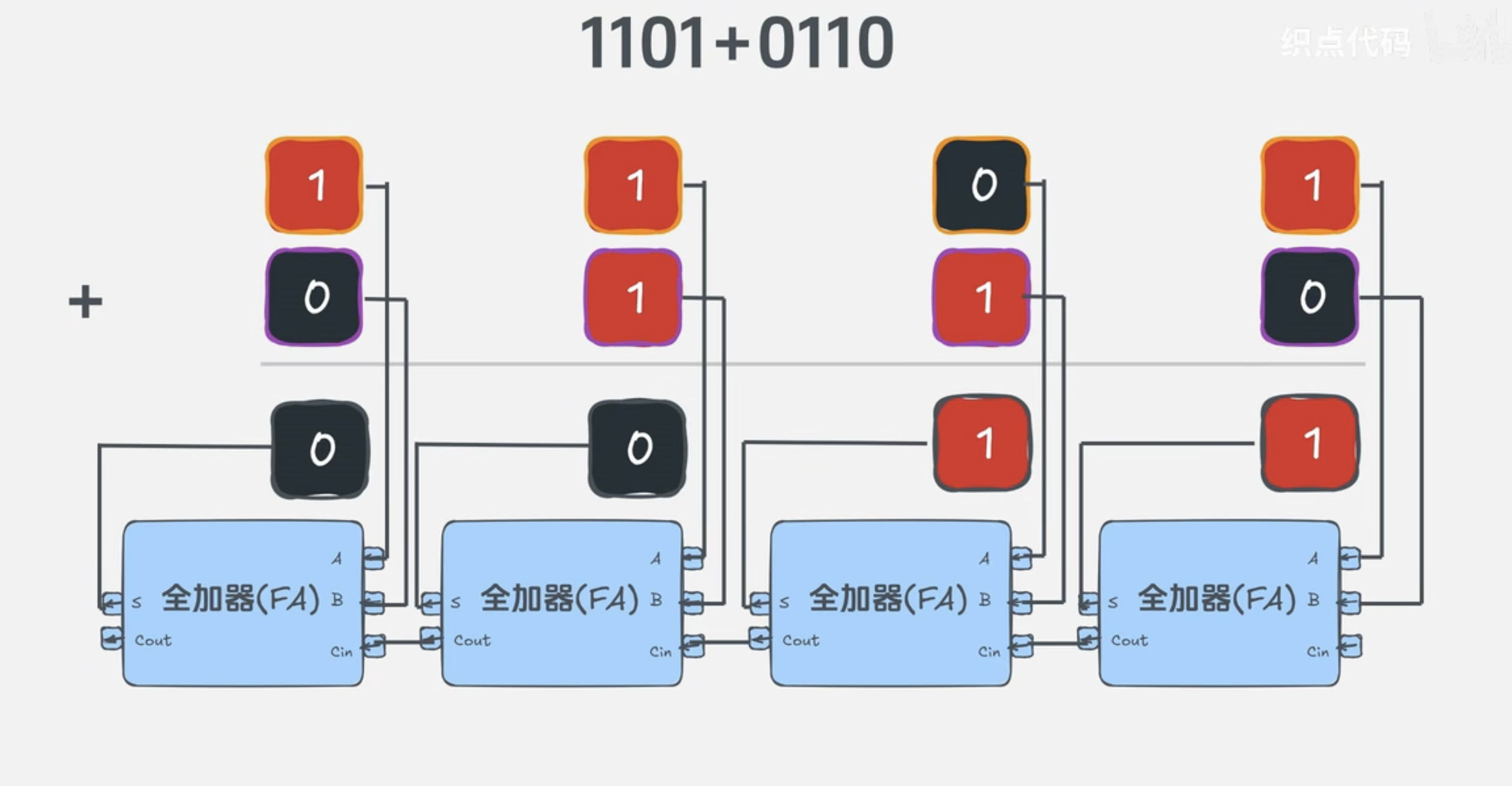

但是，我们发现这个逻辑的完成高位需要等待低位计算完成后才能进行（因为是串行计算）。 这样的话效率会比较低。我们换其他的方法。 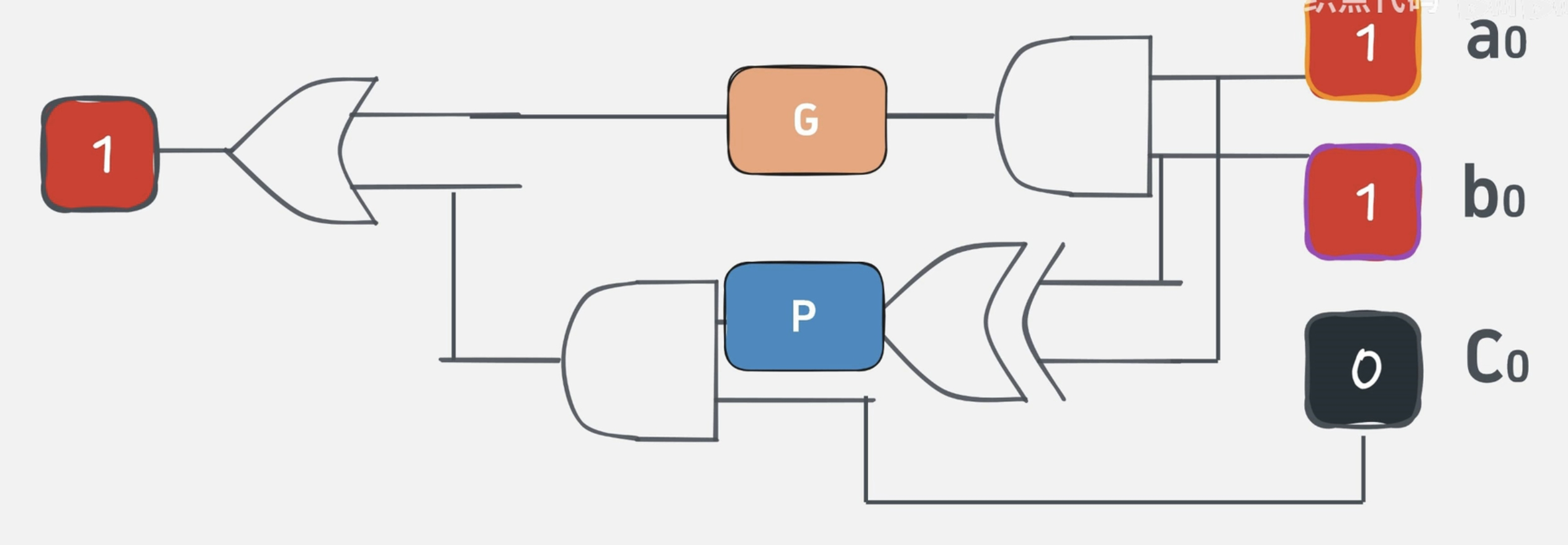在这里我们使用了逻辑表达式。

$$C_{i+1} = G_i + P_i C_i$$

通过这个我们可以算出第一位的进位：

$$C_1 = G_0 + P_0 C_0$$

然后第二位的进位：

$$C_2 = G_1 + P_1 C_1 = G_1 + P_1 (G_0 + P_0 C_0) = G_1 + P_1 G_0 + P_1 P_0 C_0$$

第三位的进位等等。

$$C_3 = G_2 + P_2 C_2 = G_2 + P_2 G_1 + P_2 P_1 G_0 + P_2 P_1 P_0 C_0$$

我们根据这个逻辑运算表达式设计电路即可。 我们发现每每高1位就要增加一个与门。但是整体的计算时间是并行的，所以效率会大大提升。

我们把这个作为一个模块封装，称为**并行加法器（*4）**。

然后我们可以再次对这些并行加法器串联起来，形成更高位的加法器。 当然为了降低延迟，我们同样可以再一次封装做成并行加法器（*x）。

最后我们可以得到一个x位的加法器。

现在我们解决了加法器的问题，下面我们要解决负数的问题.

负数表示

我们使用补码来表示负数。

• 原码：符号位+数值位
• 反码：符号位不变，数值位按位取反
• 补码：反码+1

原理：计算机中加法器是最简单的电路，所以我们使用补码来表示负数，这样我们就可以直接使用加法器来进行减法运算。

• 例：+3的原码、反码、补码

  0 0 1 1
  0 0 1 1