为什么卷积神经网络应用到图片识别上

输入特征多

图片是由像素构成，现在的手机拍摄的相片都有几千万像素。黑白图片每个像素只有一个灰度值。彩色图片每个像素有（R,G,B）三个值，分别代表红、绿、蓝。 如果一个图片长宽为1000x1000个像素的彩色图片，如果我们构造一个神经网络来处理这个图片，它的输入特征有300万个，如果隐藏层为1000个神经元，输出层为1个神经元，那么这个网络将有30亿个参数，以Float32来存储，模型大小为12GB。这么大的模型推理一次的运算代价是非常大的。

局部性

在图像里局部区域内的像素构成了重要的特征，每个像素和它周围局部区域内的像素关系紧密。比如我们识别一只猫，只要观察这个猫在图片里的区域就可以确定，无需依赖其他地方的像素信息。如果我们用全连接神经网络，每个神经元都是和所有输入像素相连的。隐藏层的神经元判断一个特征，只需要局部像素就可以，没有必要用全部的像素。这些没有必要的连接浪费了大量的权重参数。

平移不变性

不论一只猫在图片的左上角还是右下角。都不改变它是一只猫的语义信息。在计算机视觉中，语义信息（semantic information）是指图像中所表达的高层次、具有人类可理解意义的内容。如果我们训练了一个神经元，它可以接入局部的像素信息，识别一个猫，那么它就可以被重复使用，识别图片任意区域的猫。

卷积神经网络

通过n*n的滑动窗口和卷积核对图像进行卷积操作，提取图像的局部特征，从而实现图像识别、分类等任务。

在滑动窗口 * 卷积核，也要经过像之前神经网络一样的连接，相乘，激活函数得到输出结果。（特征图）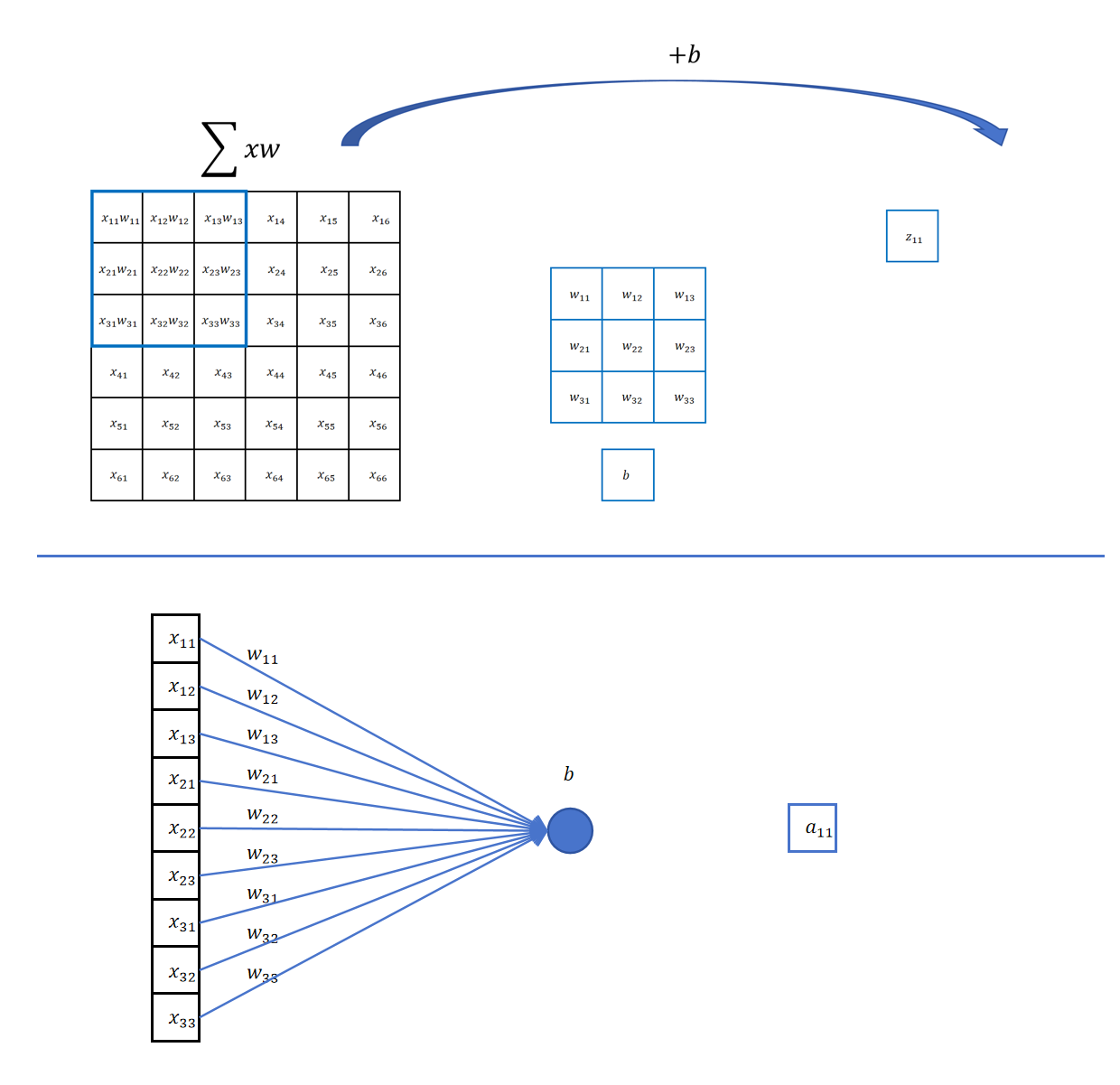

相关信息

注意：如果输入是三通道的，那么卷积核也应该是三通道的 比如： 输入28283，卷积核333 ，同时偏置为b 每一个通道对应卷积核的一个通道进行卷积操作，最后将三个通道的结果相加，再加上偏置b，得到输出结果（最后我们得到的结果应该是结合这三个通道的单通道结果）

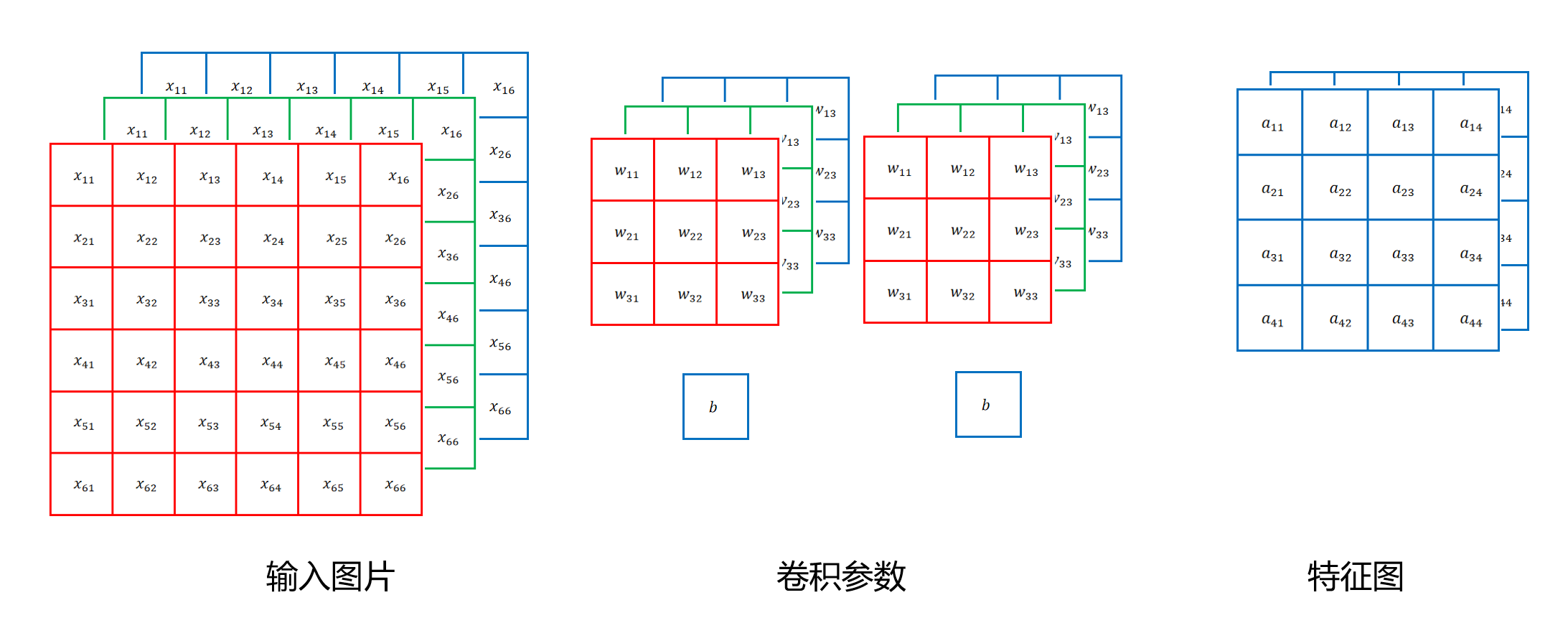
当然，一张图片我们可能要检测多个特征，那么需要的卷积核也会有多个，比如我们需要检测5个特征，那么就需要5个卷积核，最后输出的结果就是5个单通道的结果。

感受野

感受野（Receptive Field）是指在卷积神经网络中，某一特定神经元所能“看到”的输入图像区域。通过逐层的卷积和池化操作，感受野会逐渐增大，使得高层神经元能够捕捉到更大范围的上下文信息。

在卷积神经网络中，感受野的大小与卷积核的大小、步幅（stride）以及网络的深度有关。一般来说，卷积核越大、步幅越大、网络层数越深，感受野就越大。

感受野的概念对于理解卷积神经网络如何提取图像特征非常重要。通过合理设计网络结构，可以使得高层特征能够综合低层特征的信息，从而更好地进行图像分类、目标检测等任务。

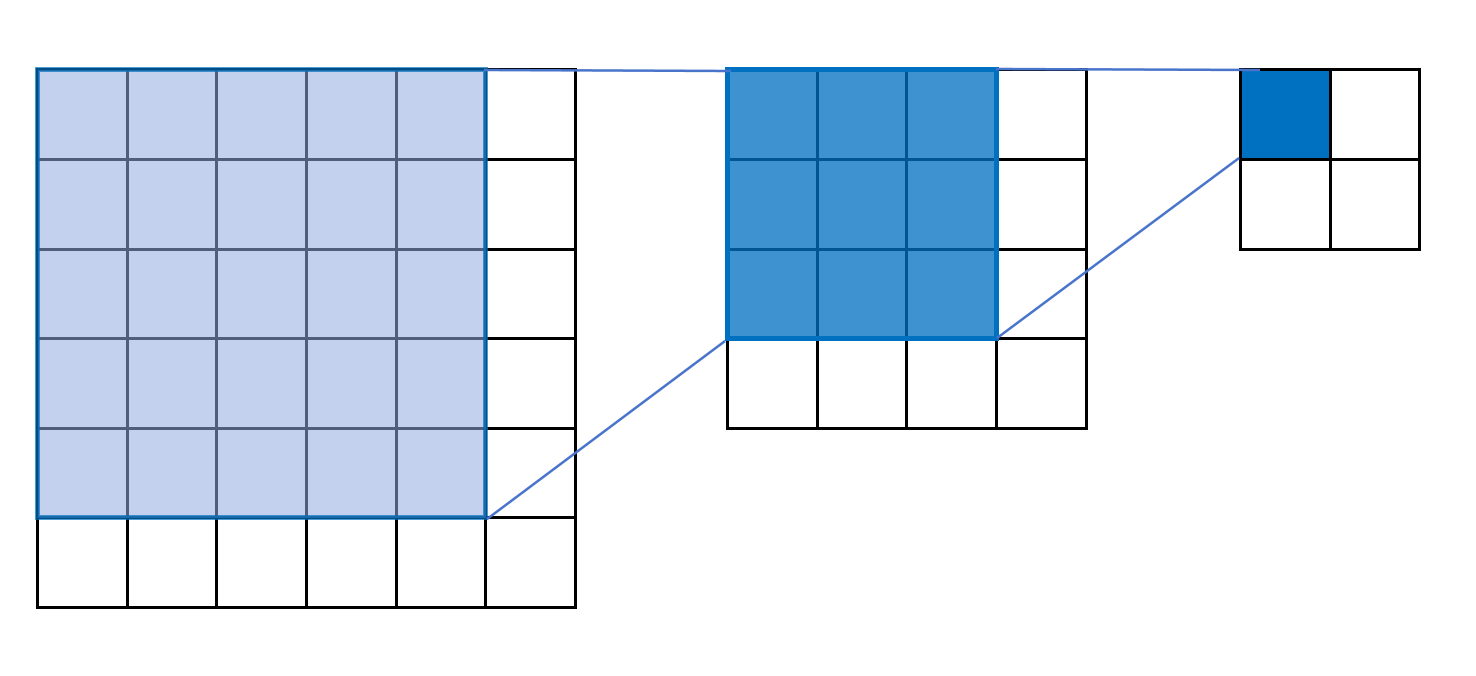
比如图中，第一个感受野3*3，后面的感受野5*5。 感受野也可以说是参与计算的像素点。

我们发现越到后面，特征图会越来越小，感受野越来越大

卷积核的大小一般设置为奇数正方形，现在我们一般取3*3的卷积核，因为它可以覆盖中心像素周围的8个像素点，能够有效捕捉局部特征，同时计算复杂度较低。

步长

一般为1，如果卷积核大，步长可以大一点。

就比如如果你的卷积核是7*7，你可以设置步长为2或者3，这样可以减少计算量，同时也能覆盖更多的区域。

如果你设置的是3*3，如果检测特征比较小，步长为1更合适。

卷积操作的问题

但是如果我们设置了卷积层，往往通过三层，就变得特别小。所以需要一个办法，不改变特征图的尺寸

同时，处于边缘的像素点在滑动窗口计算中计算的次数会比较少。

问题导入

所以我们为了解决这个问题，我们引入了 Padding 概念。

Padding: 在输入图像的边缘添加额外的像素行和列，通常这些像素的值设为0（称为零填充）。这样可以在卷积操作时保留边缘信息，并且控制输出特征图的尺寸。

特征图尺寸计算

输入：$W_{in},H_{in}$

卷积核尺寸：K

填充值：P

步长：S

输出尺寸：$W_{out},H_{out}$

计算公式$W_{out}=\frac{W_{in}+2P-K}{S}+1$

注意：有可能有的时候会不是整数，这个时候我们一般向下取整 所以实际输出一般向下取整：

$W_{out}=\left\lfloor\frac{W_{in}+2P-K}{S}+1\right\rfloor$

特别的，如果我们要保证输入输出形状一致，如果我们的$S=1$,$W_{out}=W_{in}$, $H_{out}=H_{in}$, 这就要求:

$$W_{in}=1+2P+H_{in}-K$$