比如说一个模型：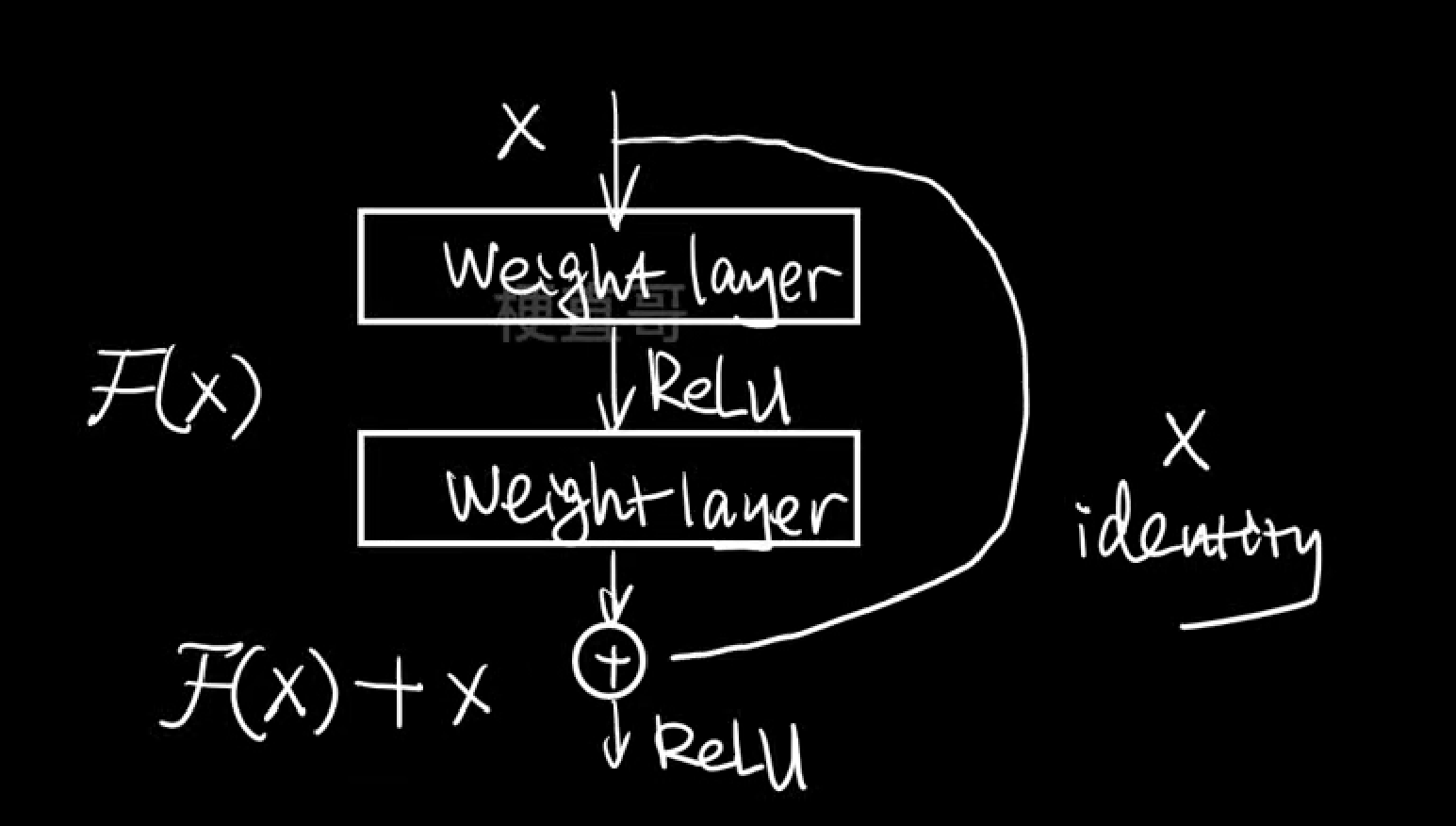

找到关于$w_{1}$的导数：

$$\frac{\partial E}{\partial w_{1}}=\frac{\partial E}{\partial y}\cdot\frac{\partial y}{\partial x_{4}}\cdot\frac{\partial x_{4}}{\partial y_{3}}\cdot\frac{\partial y_{3}}{\partial x_{3}}\cdot\frac{\partial x_{3}}{\partial y_{2}}\cdot\frac{\partial y_{2}}{\partial y_{1}}\cdot\frac{\partial y_{1}}{\partial x_{1}}\cdot\frac{\partial x_{1}}{\partial w_{1}}\\=\frac{\partial E}{\partial y}\cdot f^{\prime}(x_{4})\cdot w_{4}\cdot f^{\prime}(x_{3})\cdot w_{3}\cdot f^{\prime}(x_{2})\cdot w_{2}\cdot f^{\prime}(x_{1})\cdot x$$

整理一下：

$$\frac{\partial E}{\partial y}\cdot f'(x_4) \cdot f'(x_3) \cdot f'(x_2) \cdot f'(x_1) \cdot w_4 \cdot w_3 \cdot w_2 \cdot x$$

假设$f=\text{sigmoid}$,那么：

在导数稍微大一些会发现越来越小，几个f的导数相乘会小得不得了，这就是梯度消失。

同样的，当几个权重相乘时，梯度会特别特别大，导致梯度爆炸。

这两种梯度失真很有必要避免，触发原因就是连乘效应。 当权重不合理激活函数不合理，更会导致问题的加重。

• 梯度消失，导致更新及其缓慢，相当于无法更新，直接导致网络退化
• 梯度爆炸，导致网络不稳定。

解决方案-激活函数：Relu

$$\begin{aligned} \text{Relu}(x) &= \max(0, x) \\ \frac{\partial \text{Relu}(x)}{\partial x} &= \begin{cases} 0 & x < 0 \\ 1 & x \geq 0 \end{cases} \end{aligned}$$

虽然在$x=0$不可导，但是总体还是不错的

解决方案-梯度剪切：

解决梯度消失和爆炸问题的一种方法是梯度剪切。梯度剪切是指在反向传播过程中，将梯度值限制在一个范围之内，以防止梯度值过大或过小，从而防止梯度爆炸或消失。 减轻变化幅度。

解决方案-改进网络结构：

如：使用残差神经网络（即大名鼎鼎的ResNet）

可以跳线连接两个隐藏层，减少连乘影响，提高模型的表达能力。