17.模型误差

约 402 字大约 1 分钟

2025-09-20

准与确

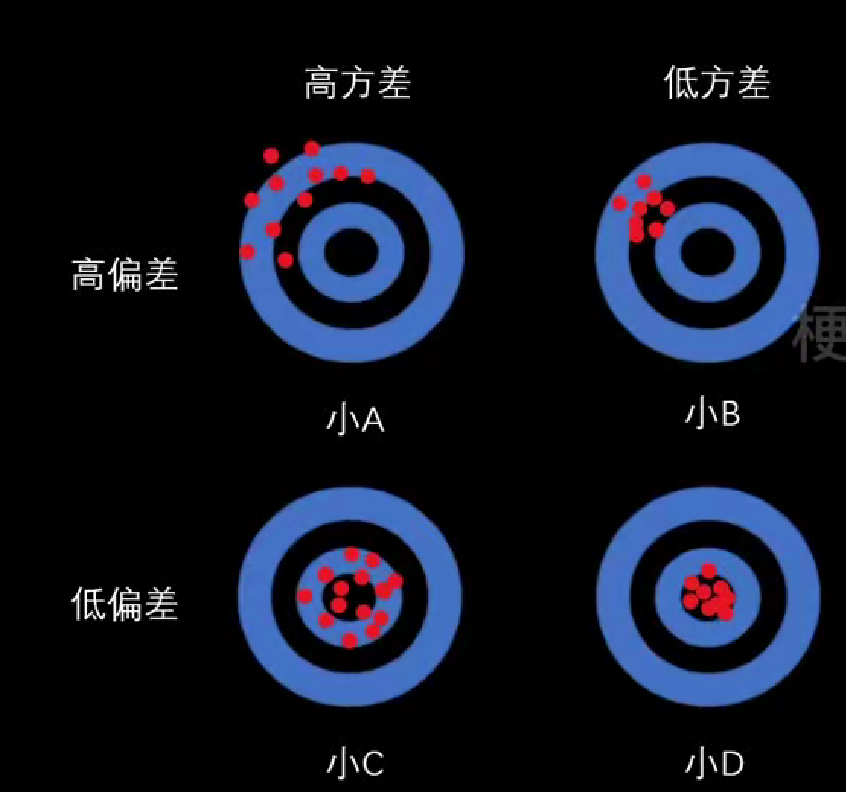
不准:都不在圆心
B和D射的比较集中,不确定

小A:不准不确

小B: 确但不准

小C:准但不确

小D:准确

由上面表示,看出: 假定测试样本为 $x$ , $f(x;D)$ 表示在训练集D上x训练的模型,真实标签记为 $y$ ,预测标签记为 $y_D$ .

偏差:预测结果的准确程度 $\text{Bias}^2(x)=[\bar{f}(x)-y]^2$

注:这里平方是因为有正有负在里面,平方消除负号影响

方差:预测结果的集中程度 $\text{Var}(x)=[\frac{1}{N}\sum_{i=1}^N(f(x_i;D)-\bar{f}(x))^2]$

噪声:任务期望的下界 $\text{Noise}(x)=E[(y_D-y)^2]$

模型误差 = 偏差 + 方差 + 无法避免的噪声

偏差 = 算法拟合能力

方差 = 数据抗扰动能力

如:用线性模型拟合非线性数据

噪声数据影响

一般情况下方差和偏差是相互冲突的.

随着训练程度的进行,方差会一直变大(数据量一直变大,平方项>=0),偏差会越来越小,所以总体误差曲线是先下降后上升的.

后面越来越敏感,越来越容易过拟合.