18.正则化
约 449 字大约 2 分钟
2025-09-20
英文名为Regularization,其实就是规范化的意思,名字取得有问题.
任何函数都可以用多项式逼近思想来近似.
f(xi)=j=0∑najxij
可以想到高等数学的泰勒展开式.比如说,我们仿造函数f(x)=sinx
sinx≈n=0∑∞(2n+1)!(−1)nx2n+1
 我们发现导致第三个过拟合出现的原因,是因为把某些特殊的点也学进去了,但是显然没必要,同时它拐弯次数太多了,导致模型的复杂度太高,无法很好地泛化到新的数据上.
我们发现导致第三个过拟合出现的原因,是因为把某些特殊的点也学进去了,但是显然没必要,同时它拐弯次数太多了,导致模型的复杂度太高,无法很好地泛化到新的数据上.
而拐弯次数多,说明多项式阶数太高,所以我们需要控制高次项的系数.
我们提取所有的特征向量w=(w1,w2,w3,…,wn),问题转化为让w项数尽可能小.
刚好向量0范数(向量中非零元素的个数)可以衡量,∣w∣0=r(w).
w∗=argwminN1i=1∑NL(yi,f(xi,w))+λR(w)
前面为损失函数,称为经验风险.后面R(w)为正则化项,整体称为结构风险.
拉索回归:R(w)=∑i=1n∣wi∣
岭回归:R(w)=∑i=1n21∥wi∥2
还有两者平衡结合的方法(ρ为参数) R(w)=∑i=1n2ρ∥wi∥2+21−ρ∥w∥2
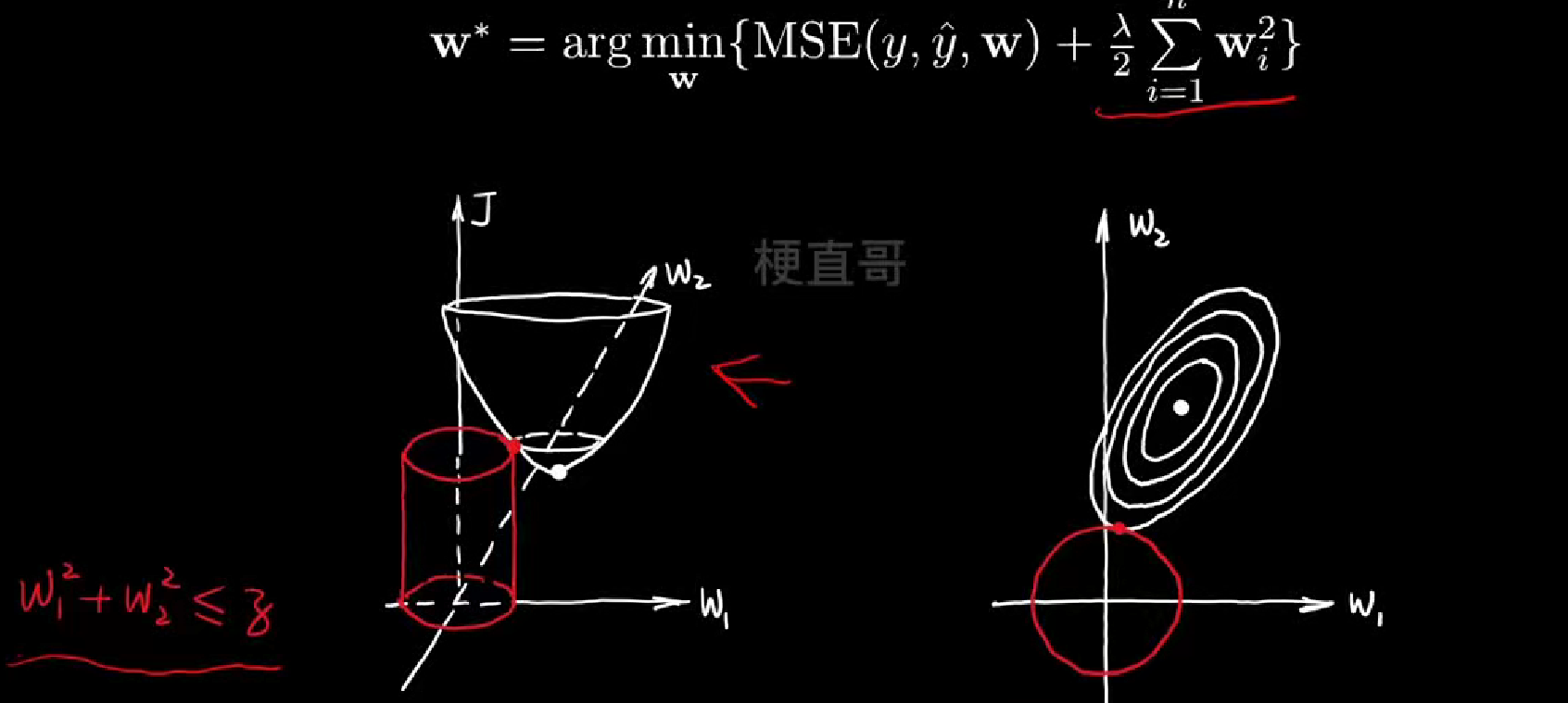
L1正则化空间解释

从图中可以看出有一个权重被干掉了,减少了复杂度
L2空间解释

