15.学习曲线
约 393 字大约 1 分钟
2025-09-20
学习曲线
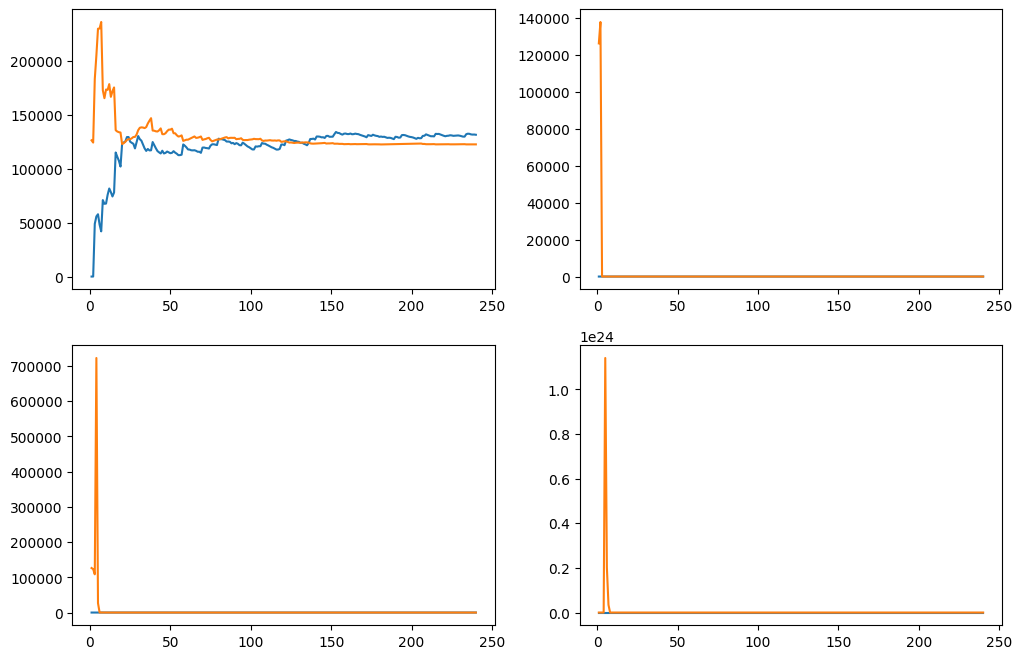
横轴是训练样本数量
纵轴是均方误差
两条曲线:分别为训练集和测试集的学习曲线.
一般情况下,训练集从0逐渐升高,测试集从很高的地方下降,最终两个曲线趋向平稳到一个值.
import numpy as np
import matplotlib.pyplot as pltX = np.linspace(-20,20,300)
y = 3*X**2+5*X+np.random.randn(300)from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)欠拟合和过拟合
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
plt.rcParams['figure.figsize'] = (12,8)
degrees = [1,2,5,20]
for i,degree in enumerate(degrees):
poly_features = PolynomialFeatures(degree=degree)
X_poly = poly_features.fit_transform(X.reshape(-1,1))
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
y_pred = lin_reg.predict(X_poly)
plt.subplot(2,2,i+1)
plt.scatter(X,y,color='red')
plt.plot(X,y_pred,color='blue')
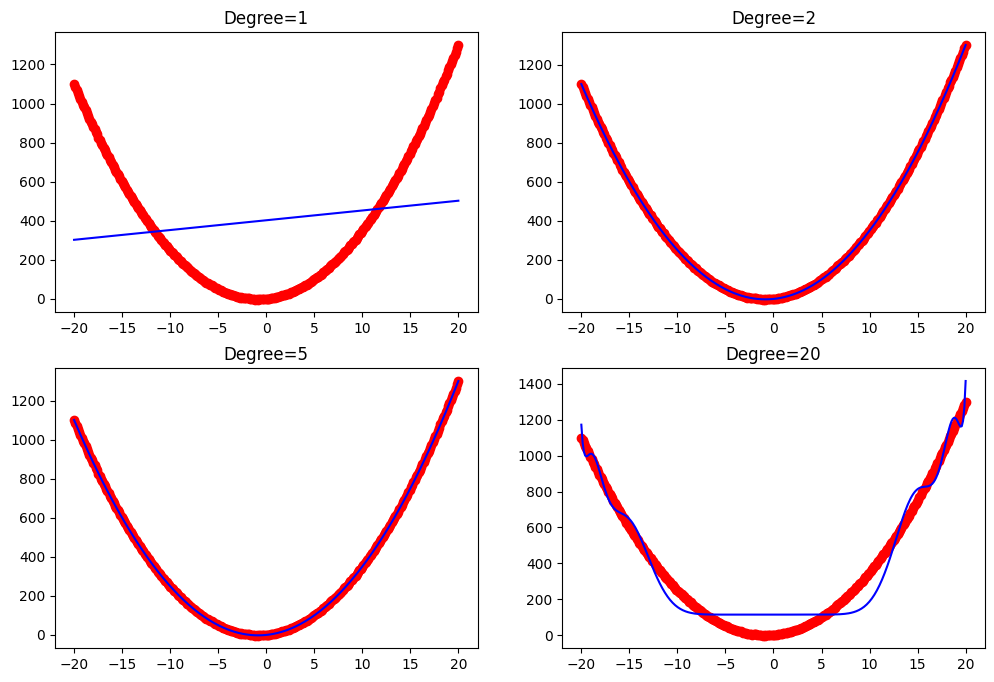
plt.title('Degree='+str(degree))
print(f'Degree {degree} R-squared: {lin_reg.score(X_poly,y)}')运行结果
Degree 1 R-squared: 0.025238281141967578 Degree 2 R-squared: 0.9999919707855061 Degree 5 R-squared: 0.999992001004748 Degree 20 R-squared: 0.955184225590763
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
plt.rcParams['figure.figsize'] = (12,8)
degrees = [1,2,5,20]
for i,degree in enumerate(degrees):
poly_features = PolynomialFeatures(degree=degree)
x_poly_train = poly_features.fit_transform(x_train.reshape(-1,1))
model = LinearRegression()
train_error,test_error = [],[]
for k in range(len(x_poly_train)):
model.fit(x_poly_train[:k+1],y_train[:k+1])
y_pred_train = model.predict(x_poly_train[:k+1])
y_pred_test = model.predict(poly_features.fit_transform(x_test.reshape(-1,1)))
train_error.append(mean_squared_error(y_train[:k+1],y_pred_train))
test_error.append(mean_squared_error(y_test,y_pred_test))
plt.subplot(2,2,i+1)
plt.plot([k+1 for k in range(len(x_poly_train))],train_error,label='train error')
plt.plot([k+1 for k in range(len(x_poly_train))],test_error,label='test error')
plt.show()